Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved exampleFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph tan^2 x sec^2 x 1 (sec x 1)(sec x 1) = = 1 sec x sec x 1 sec x 1 sec x 1 = 1, sec x = 2, cos x = 1/2, x = 60 Balas Hapus Balasan Unknown 31 Agustus 21 51 maaf tidak tau Hapus Balasan Balas Balas Unknown 19 Februari 16 10
Find The Period Of Tan 2x Class 10 Maths Cbse
Tan 2x 4
Tan 2x 4-Identity\\sin(2x) identity\\cos(2x) identity\\tan(2x) multipleangleidentitiescalculator identity \tan(2x) en Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions ) If you've ever taken a ferris wheel ride then you know aboutI need to prove this identity tan^2xsin^2x = tan^2xsin^2x start with left side tan^2xsin^2x =(sin^2x/cos^2x)sin^2x =(sin^2xsin^2xcos^2x)/cos^2x




How Many Solutions Exist For The Equation Tan 2x Tan X 0 If Pi Less Than X Less Than 2pi Study Com
View Vinod Vanganur's profile on LinkedIn, the world's largest professional community Vinod has 5 jobs listed on their profile See the complete profile on LinkedIn and discover Vinod'sUsing my 50 years old pocket calculator which isYou can put this solution on YOUR website!
The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x; The solution you were presented is surely wrong, or at least would require further explanation of context It does not make sense to have a solution outside the domain of definition of the involved expressions
Example 22 Solve tan 2x = – cot (x" " 𝜋/3) tan 2x = –cot (𝑥" " 𝜋/3) We need to make both in terms of tan Rough tan (90° θ) = –cot θ –cot θ = tan (90° θ) –cot θ = tan (𝜋/2 " θ" ) Replacing θ by x 𝜋/3 –cot ("x " 𝜋/3) = tan (𝜋/2 " x " 𝜋/3) tan 2Tan 2x = 2tan x / 1−tan2x tan 2x = Double angle function of tan x READ How do I add a GridLayout view? 1 Another solution Consider the equation Let , use the multiple angle formulae and obtain Discrading the trivial ,we then face a quartic equation in which can be solved with radicals The solutions are all positive and the smallest is and then At this point, I am stuck;




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction
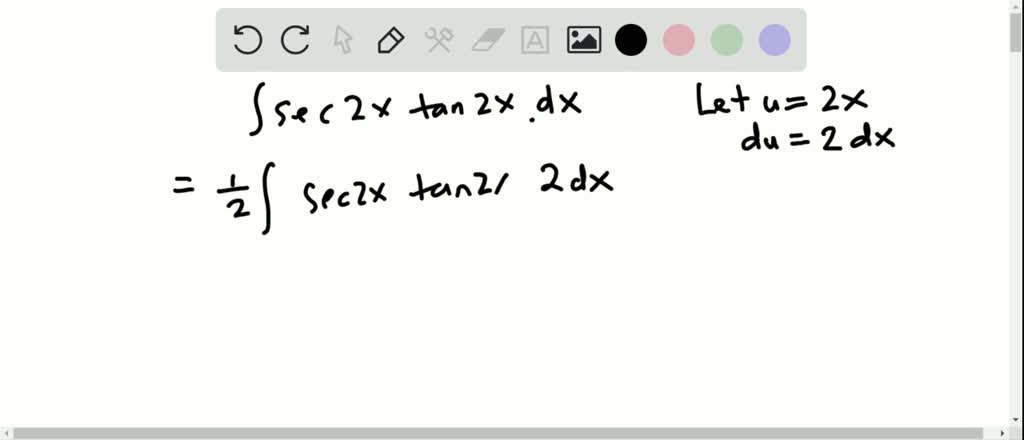



Solved Evaluate The Integral Int Sec 2 X Tan 2 X D X
I'm not sure if I should be working on the right side of the equation instead! What is the derivative of #tan^2 x#?Tan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formula




15 Find Sin 2x Cos 2x And Tan 2x If Tanx And X Terminates In Homeworklib




If Cos 2x Cos 4x 1 Then Tan 2x Tan 4x 1 1 2 0 3 1 4 2
Calculus Differentiating Trigonometric Functions Derivative Rules for y=cos(x) and y=tan(x) 1 Answer Jim G #2tanxsec^2x# Explanation #"note "tan^2x=(tanx)^2# #"differentiate using the "color(blue)"chain rule"# #"given "y=f(g(x))" then"# 1tan^2(x) = 1 (sin 2 x)/(cos 2 x) = cos 2 x sin 2 x/cos 2 x = cos 2x/cos 2 x is a posibly 'simplified' version in that it has been boiled down to only cosines What is tan 2x equivalent to?



Solve The Following Equations Tan X Tan 2x Tan 3x Sarthaks Econnect Largest Online Education Community




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
Cos 2x ≠ 2 cos x;Easy as pi (e) Unlock StepbyStep Natural Language Math Input Nhung cong thuc luong giac co ban 1 CÁC CÔNG THỨC LƯỢNG GIÁC CƠ BẢN Biên soạn và thực hiện vi tính NguyÔn §øc B¸ GV THPT TIỂU LA THĂNG BÌNH I/Các hệ thức cơ bản sin 2 x cos 2 x cosx sinx π , (x ≠ kπ) , (x ≠ kπ) c otx= cosx 2 sinx 1 π 1 = 1 tan 2 x, (x ≠ kπ) 2 = 1 cot 2 x, (x ≠




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Tan 2x ≠ 2 tan x by Shavana GonzalezTan^2x/(1tan^2x) WolframAlpha As you can see it comes out to sin^2(x) You can see this yourself by reminding yourself of the definition of tan(x) and then using the identity sin^2(x)cos^2(x) = 1 With a little algebraic manipulation the result then comes out The identity, as you noted, is tan 2 x 1 = sec 2 x, for all values of x Rearranging, you absolutely get tan 2 x sec 2 x = 1 So, the original statement is false Sure, there might be values of x for which the original equation works It's solvable, but that doesn't make it true for all x




Integrate Tan 2x By Parts




How Many Solutions Exist For The Equation Tan 2x Tan X 0 If Pi Less Than X Less Than 2pi Study Com
Derivative of tan(2x)^3 Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processOnly size 1X, 2X available Rated 50 out of 5 stars Rated 50 out of 5 stars Rated 50 out of 5 stars Rated 50 out of 5 stars Rated 50 out of 5 stars ( 1 ) 361 ItemsTRIGONOMETRY LAWS AND IDENTITIES DEFINITIONS sin(x)= Opposite Hypotenuse cos(x)= Adjacent Hypotenuse tan(x)= Opposite Adjacent csc(x)=




Ii Find The General Solution Of Tan 2x 0 C Differentiate Sin X2 X W Rt X




Integrate Tan 2x
What is tan TANX?Now, we can recognise sec^2 (x) as the derivative of tan (x) (you can prove this using the quotient rule and the identity sin^2 (x) cos^2 (x) = 1), while we get x when we integrate 1, so our final answer is tan (x) x c Answered by Warren L • Maths tutorThe vertical asymptotes for y = tan ( 2 x) y = tan ( 2 x) occur at − π 4 π 4, π 4 π 4, and every π n 2 π n 2, where n n is an integer Tangent only has vertical asymptotes Use the form atan(bx−c) d a tan ( b x c) d to find the variables used to find the amplitude, period, phase shift, and




If Tan2x Tan 2 X Then The Value Of X Is




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
#d/dx(tan(2x))# will simply be #sec^2(2x)* d/dx(2x)# according to the chain rule Then #d/dx(tan(2x))=2sec^2(2x)# If you want to easily understand chain rule, just remember my tips take the normal derivative of the outside (ignoring whatever is inside the parenthesis) and then multiply it by the derivative of the inside (stuff inside the parenthesis)IIT JEE 1999 limx → 0 ( x tan 2x 2x tan x/ (1 cos 2x)2) is (A) 2 (B) 2 (1/2) (D) (1/2) Check Answer and Solution for aboveCosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosine



A Trig Identity



Trigonometry Functions User S Blog
Tyrion101 said But is it equal to (2tanx/1tan^2x)^2 is what I'm asking I may have been unclear Yes and no means , which in turn is equal to In what you wrote, you are missing parentheses around the quantity in the denominator, 1 tan 2 (x) What you wrote is the same as #10 symbolipointTan 2x is an important trigonometric function Tan 2x formula is one of the very commonly used double angle trigonometric formulas and can be expressed in terms of different trigonometric functions such as tan x, cos x, and sin xExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Solved If Y X Tan 2x Then The Dervative Is Y 2x Sec 21 2xtan 2x 32r Sec 21 X Lan 2x 6 Y X Sec 2x 2x Tan 2x 2x Sec 2x
Integral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integral of sin(x), integDerive the expression 1 tan^2x Get the answer to this question and access a vast question bank that is tailored for students Although the expression tan 2 x contains no parenthesis, we can still view it as a composite function (a function of a function) We can write tan 2 x as (tan(x)) 2 Now the function is in the form of x 2, except it does not have x as the base, instead it




Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Ppt Download




bestpictjcry Tan 2x Tan 2x
Similar Questions trignometry tanxcotx=5 than find the value of tan^2xcot^2x arithmetic if tanxcotx=2 then the value of tan^5x cot^10x isTan^2 (x) WolframAlpha Area of a circle?GrrrrrI could get a little help from the tutors in the Math Lab on




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Imbogăţi Strigăt Te Rog Nu Tan 2x Calculator Stephadelphia Com
Get an answer for 'Prove tan^2x sin^2x = tan^2x sin^2x' and find homework help for other Math questions at eNotes Finally, just a note on syntax and notation tan (2x) is sometimes written in the forms below (with the derivative as per the calculation above) Just be aware that not all of the forms below are mathematically correct tan2x Derivative of tan2x = 2sec 2 (2x) tan 2 x Derivative of tan 2 x = 2sec 2 (2x) tan 2xTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1
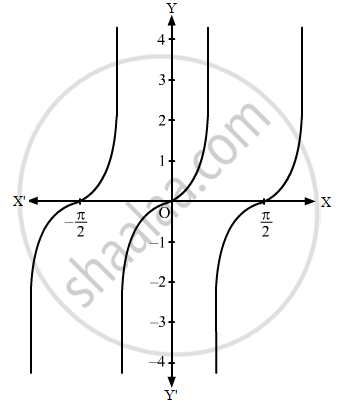



Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Proportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsSolve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2Tan^2x = sin^2x/cos^2x How do you calculate tan 2x?




Tan 2x Formula What Is Tan 2x Formula Examples



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
\tan(x) is the trigonometric function that relates the angle x to the opposite and adjacent sides of a rightangle triangle Precalculus Prove the following identities 1 1cosx/1cosx = secx 1/secx 1 2 (tanx cotx)^2=sec^2x csc^2x 3 cos (xy) cos (xy)= cos^2x sin^2yB) (tanx 1)(tanx1)/1 tan^2(x) = (sinx/cosx 1)(sinx/cosx 1) / 1/cosx then again I'm stuck!




Solved Find Sin 2x Cos 2x And Tan2x If Tanx 2 And X Terminates In Quadrant Iii Sin 2x 2 Cos 21 Tan 2x



1
View Hari Godavarthi's profile on LinkedIn, the world's largest professional community Hari has 1 job listed on their profile See the complete profile on LinkedIn and discover Hari's Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and Get an answer for 'Verify tan^2x sin^2x= (tan^2x)(sin^2x)' and find homework help for other Math questions at eNotes




Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby




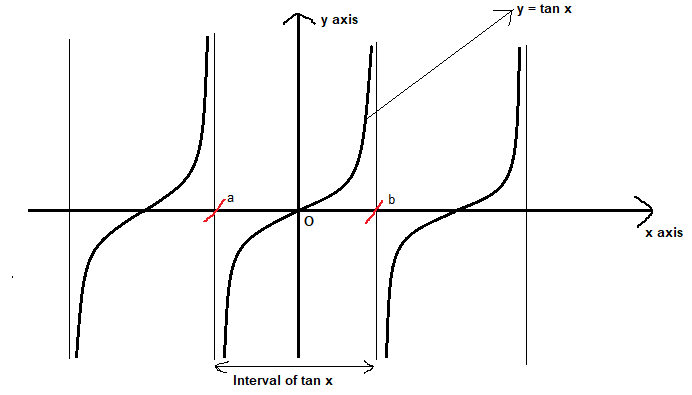
Find The Period Of Tan 2x Class 10 Maths Cbse
Therefore, the values of sin(2X), cos(2X) and tan(2X) are – √35 / 18, 17 / 18 and – √35 / 17 respectively Similar Questions Question 1 Find sin(2X),cos(2X) and tan(2X) from given information secX = 8, X lies in Quadrant IVMultiply top by (1 tan^2(x)) to get tan^4 (x) 1 or (tan^2(x)1)(tan^2x1) then i'm stuck!Sin 2x Formula in Terms of Tan We can write the formula of sin 2x in terms of tan or tangent function only For this, let us start with the sin 2x formula sin 2x = 2 sin x cos x Multiply and divide by cos x Then sin 2x = (2 sin x cos 2 x)/ (cos x) = 2 (sin x/cosx ) (cos 2 x) We know that sin x/cos x = tan x and cos x = 1/ (sec x)



What Is The Formula Of Tan2x Quora




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
How to find the integral of tan(2x)In this tutorial we go through the steps to find the integral of tangent(2x) using the usubstitution integration method
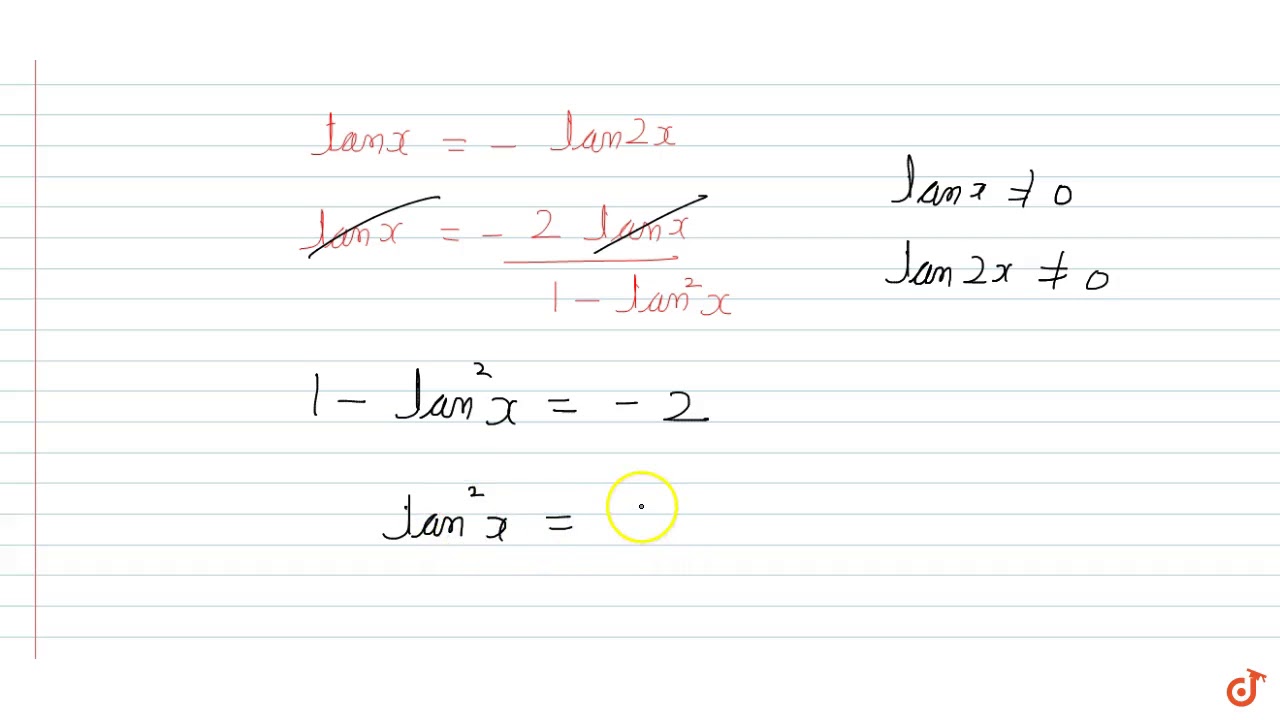



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube




Solve Tan 2x 2sinx 0 Maths Trigonometric Functions Meritnation Com
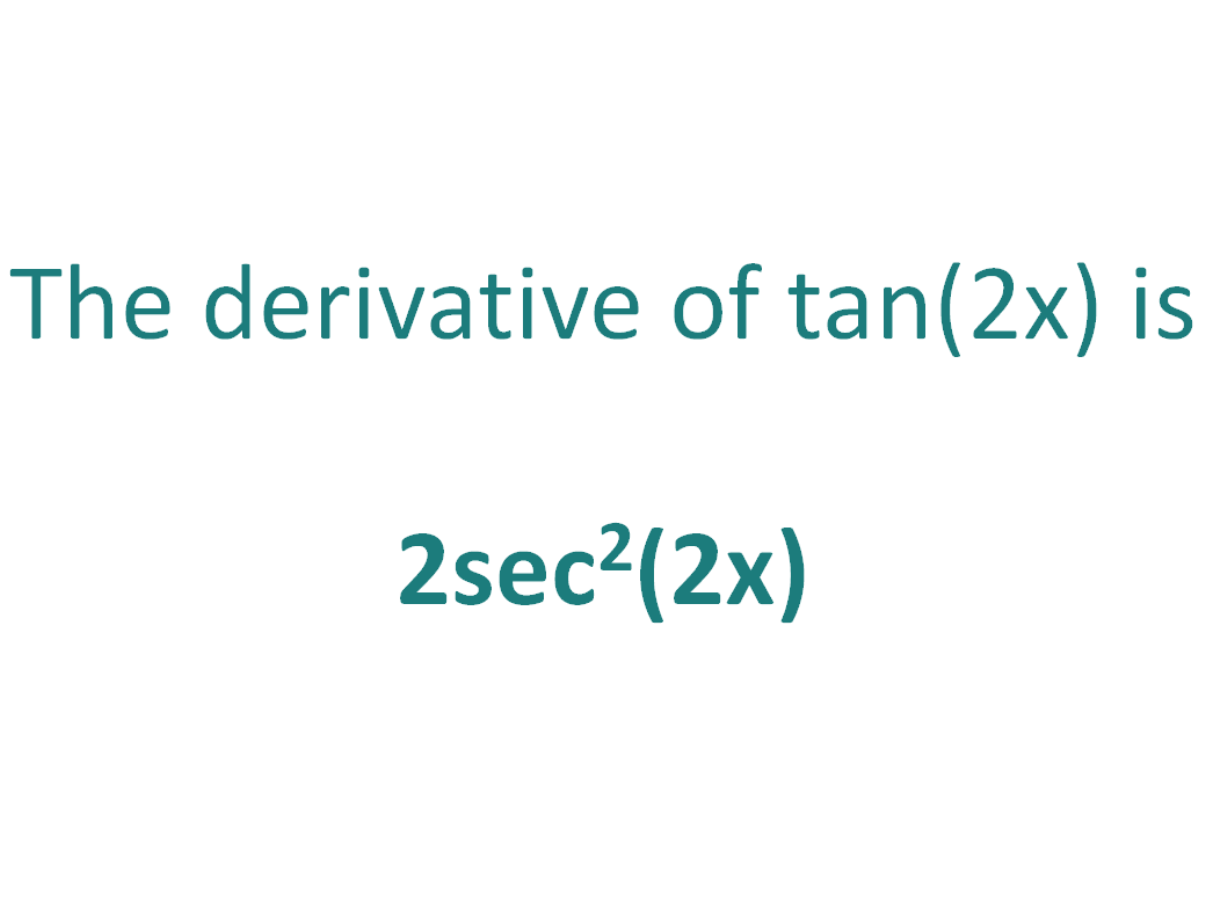



The Derivative Of Tan 2x Derivativeit



What Is Integral Of Sin2x Tan2x Quora
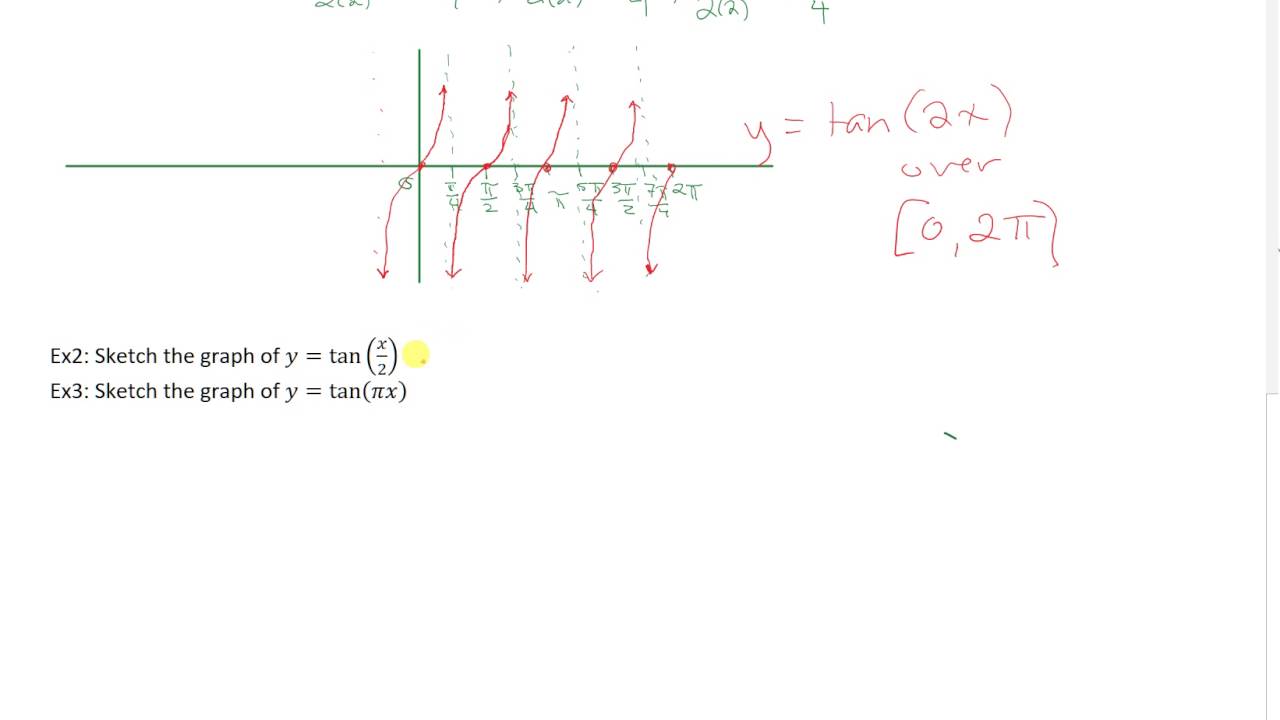



Sketching Y Tan 2x And Y Tan X 2 Youtube
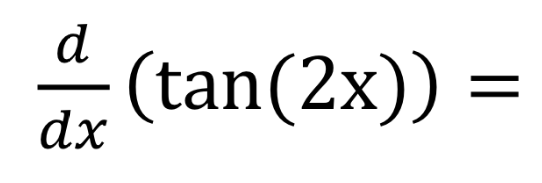



Solved D Dx Tan 2x Chegg Com




Please Write Legibly Find Sin 2x Cos 2x And Tan 2x If Tanx And Homeworklib




In This Solution Why The 2 Tan2x 1 Tan 2x Was Dived By1 2tan 2x 1 Tan 2x 2 Trigonometric Functions Q23 Prove That Solution 4tanx La Tan X Maths Trigonometric Functions Meritnation Com



What Is The Value Of Tan2x Tan4x 1 Find Tan3x Quora
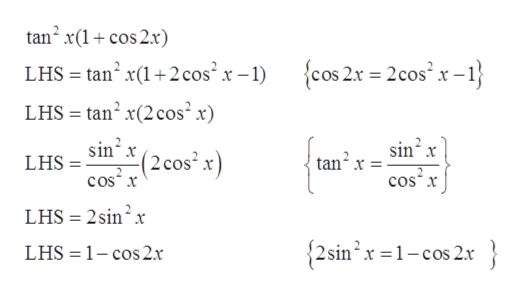



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby



Sin 2x Cos 2x And Tan 2x




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
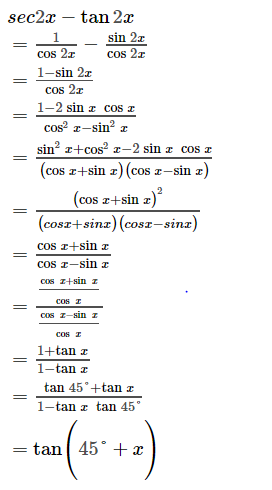



Sec2x Tan2x If0 X P 4




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




Example 22 Find Derivative Of Tan 2x 3 Chapter 5 Class 12




View Question Find Sin 2x Cos 2x And Tan 2x From The Given Information Tan X 1 2 Cos X 0




What Is The Integration Of Tan 2x Solution Quora




The General Solution Of The Equation Tan 2x 1 Is




Integrate Sec 2x Method 1




Cbse Class 11 Sin 2x Sin 3x Cos 2x Cos 3x Tan 2x Tan 3x Offered By Unacademy




Sec 2x Tan 2x Math




Tan2x ただの悪魔の画像
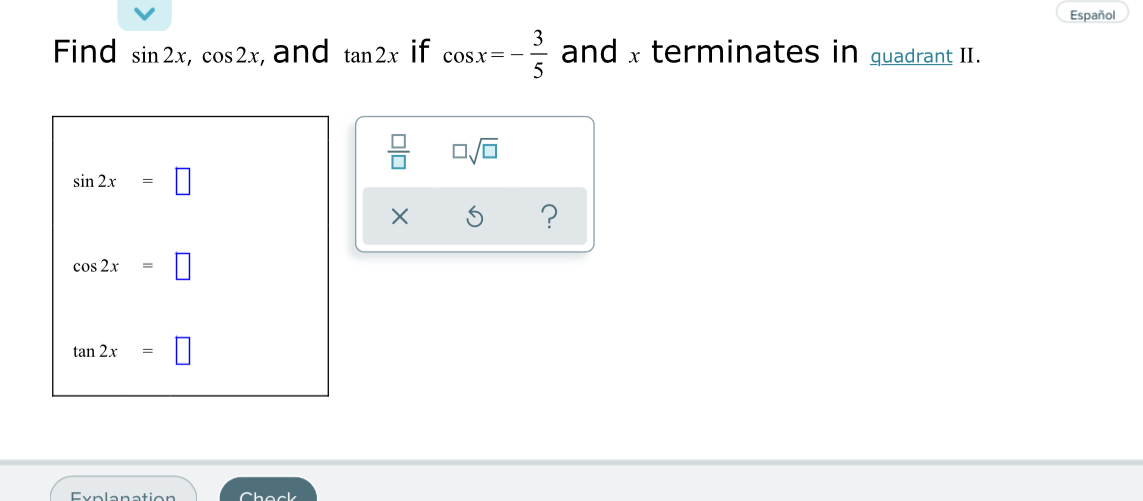



Answered 3 Find Sin 2x Cos 2x And Tan 2x If Bartleby
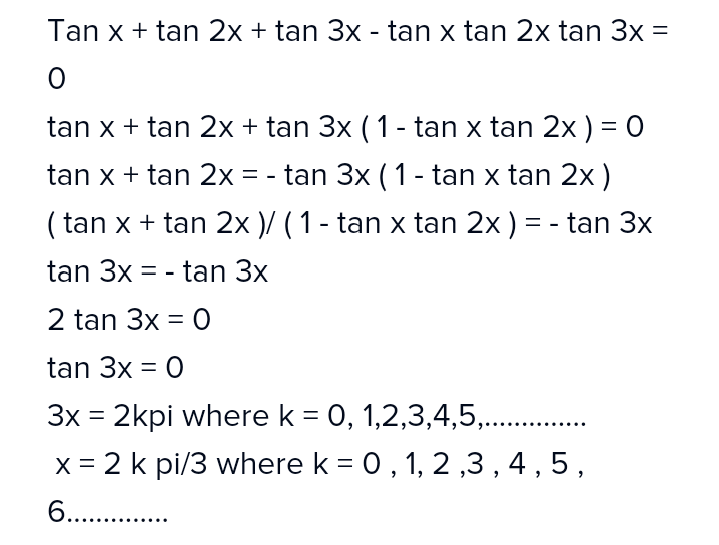



Solve Tanx Tan2x Tan3x Tanxtan2xtan3x



Find The Derivative Of The Function Tan 2x 3 From The Definition First Principles Sarthaks Econnect Largest Online Education Community




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How To Graph Tan Ex Y Tan2x Study Com




Answer The Following Questions Find The General Solution Of Tan 2x 0 Youtube




Solved Sketch The Graph Of The Following Functions Y Tan 2x Y Self Study 365
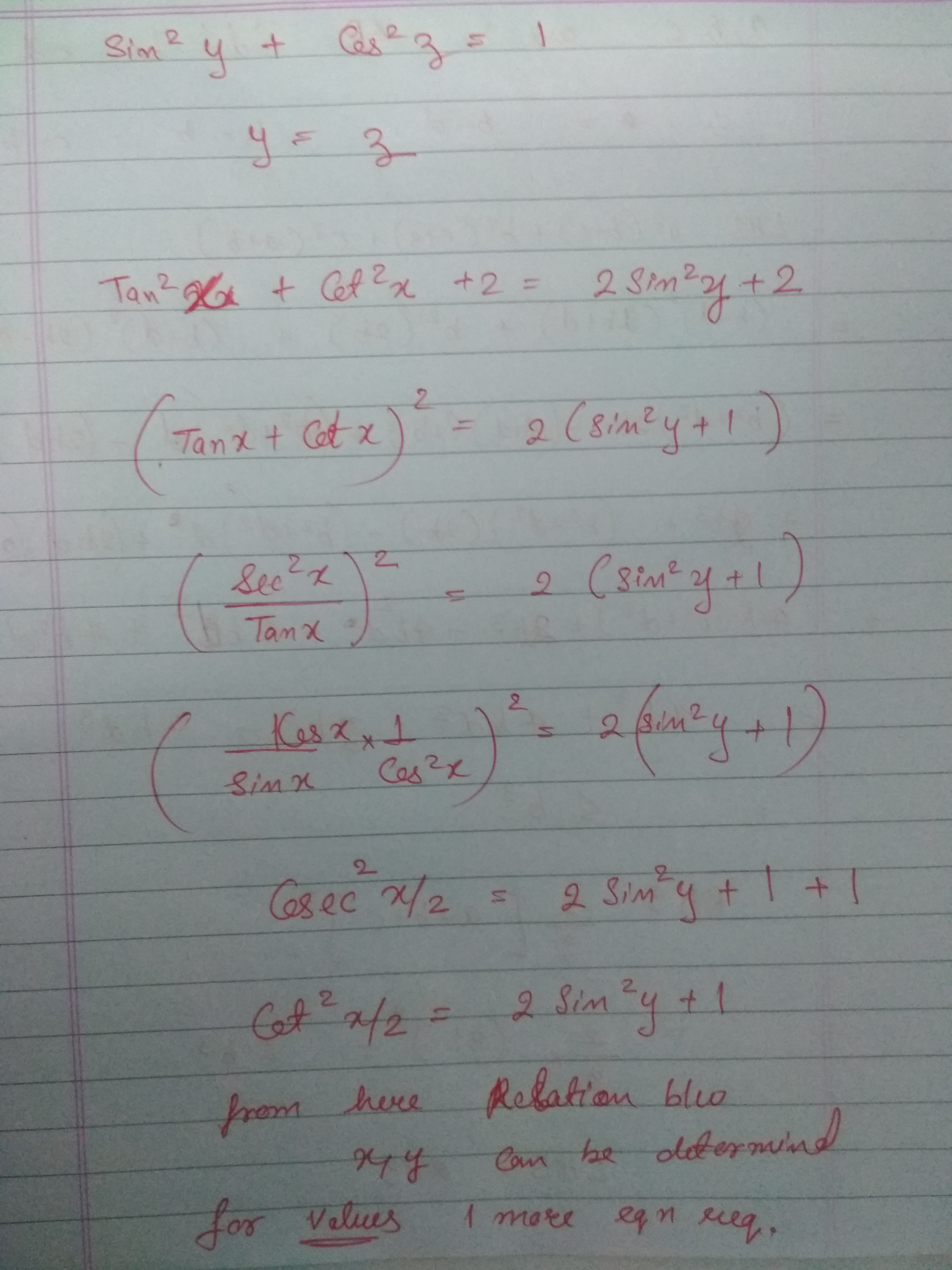



Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians



1
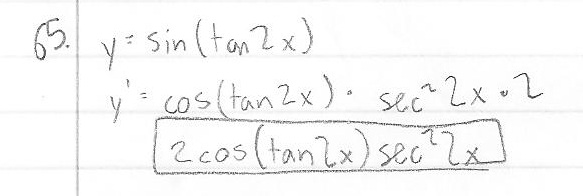



いろいろ Tan2x 1sec2x ただの悪魔の画像



Math Problems Simplifying With Trigonometry Identities And Then Integration




Integral Of Tan 2x Formula Proof Examples




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



1



Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com



What S The Integral Of Tan 2x Quora




Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




The Value Of F 0 If F X X Tan 2x Sin3x Sin5x Is Continuous At X 0 Is




Tangent For Sum Of Double Angle Shortmath




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines




Differentiate The Following From First Principle Tan 2x



Tan2x 1 ただの悪魔の画像



Solve For X Tan 2x 65 Cot 3x 15



Solution Determine The Period Of Y Tan 2x




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




05 Derivative Of Tangent Function Tan2x And Tanx 2 Youtube



Solved Explian The Proof For This Tan 2x 1 Tan X Co5 2x Solution Starting With The Left Side Sin 2x Sm X Step 1 Cos 2x Cos X Sin 2x Course Hero




Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com
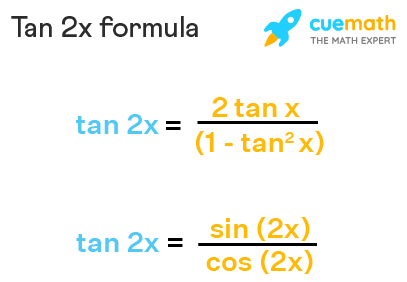



Tan 2x Formula What Is Tan 2x Formula Examples
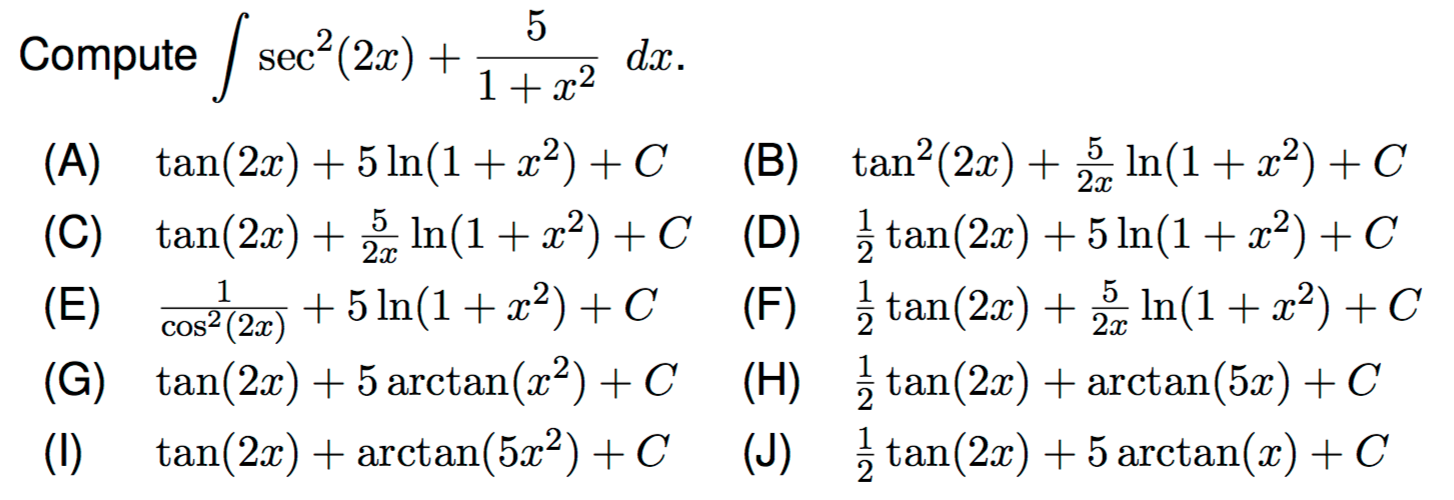



Solved Compute Sec 2 2x 5 1 X 2 Dx A Tan 2x 5 Ln L Chegg Com



1



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib
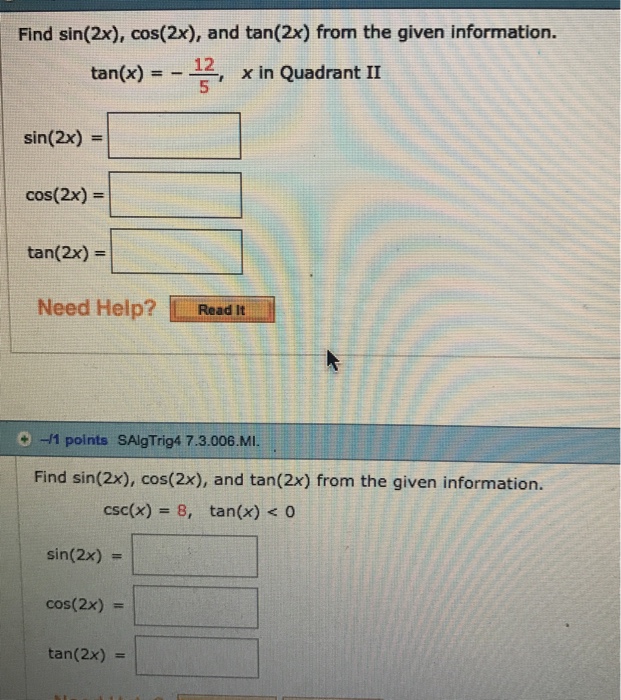



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Solved Which Of The Following Is Equivalent To Tan 2x 3y Chegg Com



bestpictkt8j 無料ダウンロード 1 Tan 2x 1 Cot 2x Tan 2x 1 Tan 2x 1 Cot 2x Tan 2x



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre




Solved The Expression Tan 4x Tan 2x 1 Tan 4x Tan 2x Chegg Com




Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3 Check All That Apply Options Are In Brainly Com



Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints



Solved Determine Exact Value Of Tan 2x Sin2x And Cos2x If Cscx 17 15 And X 3 2 Course Hero




Differentiate The Following From First Principle Tan 2x 1




Trig Identity Sec2x Minus Tan2x T10 Youtube



Differentiate The Sec 1 1 Tan 2x 1 Tan 2x W R T X Sarthaks Econnect Largest Online Education Community




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



0 件のコメント:
コメントを投稿